The “Mississippi” challenge from Vector 18.2

This example is taken directly from Norman Thomson's J-ottings column in Vector 18.2. It is an interesting comparison of the speed of the 'obvious' outer-product solution and a very sneaky algorithm using upward ranking.

ã The Mississippi challenge (from Vector 18.2 - Jottings)
ã The object is to take a vector and return the occurrence number for each element
 s û 'mississippi' 

ã The boring way with an outer product
 nub v: { ((vÉv)=ÉÒv)/v }
 unq û nub s
 tbl û unq Ê.= s 
ã Cum across and save where we had numbers  
 tbl û tbl « +\@1 tbl   
 oc û ¢1++/tbl

'The answer is ',îoc

ã Make it a function so we can time it ...
 oca s : { tbl û (nub s)Ê.=s ; tbl û tbl « +\@1 tbl; (+/tbl)-1}

ã Now for the super-sneaky approach (J-forum written up in Vector)
 t û (sÉunq)[unqÉs]
 r û èèt
 occ û r-r[t]

'The answer is also ',îocc

ã Get a little nearer the J style using index ...
 t û (unqÉs)#sÉunq
 r û èèt
 occ û r-t#r

'The answer is still ',îocc 

ã Finally as a function
 ocb s: { uûnub s; tû(uÉs)#sÉu; rûèèt; r-t#r }

' oca s   ã tests the boring one'
' ocb s   ã tests the sneaky version'
' '
'Try some timings with various sized arrays ...' 
' time qq := ocb 500000 rho s   ã Arthur wrote a mean gradeup here!'

The timings are interesting, when we run this in A+ and in the two major Windows APLs:

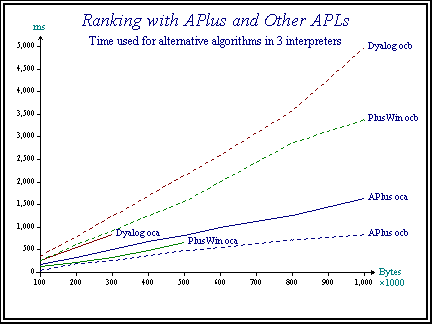
The outer-product solution is actually the faster of the two algorithms in both Dyalog and +Win, but it runs out of memory fairly quickly in my standard setup of 20M. In A+ it shows very comparable timings, but of course you now have 'infinite' memory as A+ will just grab swapfile on your hard-drive as it needs to allocate space for ever bigger arrays.

The significant line is the bottom one which supports the claim in Jonathan Barman's first impressions of A - that sorting is impressively fast. This set of timings is definitely curving downwards, so the elapsed time is less than linear with the size of the array, which is very impressive.

© British APL Association 2001
Please send any comments to Adrian Smith via adrian@causeway.co.uk - thank you.