Statistical Methods
Discovered by the Power of APL
Through its array functionality APL can treat masses of data, piled up in huge spreadsheets or databases, much more intelligently to generate meaningful perceptions, rather than just doing primitive operations such as column reductions.
Odd Man Out
Spotting the ‘odd man out’, the exceptional figure in a mass of numbers, is a recurring task of management. A simple APL technique finds and highlights anomalous figures in arrays, where human eyes are likely to overlook them. By using these results to add colour, the tables immediately gain visual appeal.
In magazines there are sometimes intelligence test with questions like this:
|
Which number does not belong?
1001 996 1000 1005 2004 998 997 999 1004 1003 |
Table 1: Magazine’s level 1 IQ question
Of course, it is easy to see that one number is twice as big as the others. Anyway, for us this indeed is a question APL can solve:
IQuestion
1001 996 1000 1005 2004 998 997 999 1004 1003
0⍕Normalize IQuestion
1 1 1 1 2 1 1 1 1 1
All we need for that is a little function which will average the values to 1. The rounding to whole numbers will then do the rest:
Normalize←{(⍵×⍴⍵)÷+/|⍵}
You do not think it should have been necessary to ask APL for a solution? Then let’s take on the next level in the contest.
|
Which number does not belong? 507 364 1196 689 611 1235 78 1001 1014 1079 78 56 184 106 94 190 12 154 156 166 2691 1932 6348 3657 3243 6555 414 5313 5382 5727 3393 2436 8004 4611 4089 8265 522 6699 6786 7221 2457 1764 5796 3339 5922 5985 378 4851 4914 5229 2886 2072 6808 3922 3478 7030 444 5698 5772 6142 2847 2044 6716 3869 3431 6935 438 5621 5694 6059 3900 2800 9200 5300 4700 9500 600 7700 7800 8300 3471 2492 8188 4717 4183 8455 534 6853 6942 7387 936 672 2208 1272 1128 2280 144 1848 1872 1992 |
Table 2: Magazine’s level 2 IQ question
I hope you could find the non-matching number! Again APL can do it for you:
Sales←(10?100)∘.×(10?100)
Sales[5;5]×←2
Sales
507 364 1196 689 611 1235 78 1001 1014 1079
78 56 184 106 94 190 12 154 156 166
2691 1932 6348 3657 3243 6555 414 5313 5382 5727
3393 2436 8004 4611 4089 8265 522 6699 6786 7221
2457 1764 5796 3339 5922 5985 378 4851 4914 5229
2886 2072 6808 3922 3478 7030 444 5698 5772 6142
2847 2044 6716 3869 3431 6935 438 5621 5694 6059
3900 2800 9200 5300 4700 9500 600 7700 7800 8300
3471 2492 8188 4717 4183 8455 534 6853 6942 7387
936 672 2208 1272 1128 2280 144 1848 1872 1992
0⍕Normalize Sales
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 2 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
Imagine that the numbers in Sales are the revenues of item groups in several regions. Then this function will show, by colouring a table, that there were far more jackets sold in Germany, when compared to other regions. It would have been difficult to get that information just by studying the numbers.
| Region \ Items | Pants | Jeans | Shirts | Skirts | Jackets | Suits | Sweater | Slippers | Sneakers | Socks |
| Austria |
507
|
364
|
1196
|
689
|
611
|
1235
|
78
|
1001
|
1014
|
1079
|
| Belgium |
78
|
56
|
184
|
106
|
94
|
190
|
12
|
154
|
156
|
166
|
| Denmark |
2691
|
1932
|
6348
|
3657
|
3243
|
6555
|
414
|
5313
|
5382
|
5727
|
| France |
3393
|
2436
|
8004
|
4611
|
4089
|
8265
|
522
|
6699
|
6786
|
7221
|
| Germany |
2457
|
1764
|
5796
|
3339
|
5922
|
5985
|
378
|
4851
|
4914
|
5229
|
| Great Britain |
2886
|
2072
|
6808
|
3922
|
3478
|
7030
|
444
|
5698
|
5772
|
6142
|
| Holland |
2847
|
2044
|
6716
|
3869
|
3431
|
6935
|
438
|
5621
|
5694
|
6059
|
| Italy |
3900
|
2800
|
9200
|
5300
|
4700
|
9500
|
600
|
7700
|
7800
|
8300
|
| Spain |
3471
|
2492
|
8188
|
4717
|
4183
|
8455
|
534
|
6853
|
6942
|
7387
|
| Sweden |
936
|
672
|
2208
|
1272
|
1128
|
2280
|
144
|
1848
|
1872
|
1992
|
Table 3: Sales chart
To handle similar variables of higher rank, it is necessary to extend the Normalize function. Now it will average one dimension after another. As averaging a further dimension changes the result of previously averaged dimensions, this needs to be iterated several times until the result becomes stable. Fortunately this algorithm converges with any number of dimensions.
Normalize←{ ⍝ Normalize an array of arbitrary rank - Dyalog V11 version
AxialNormalize←{(⍵×⍺⊃⍴⍵)÷[(⍳⍴⍴⍵)~⍺]+/[⍺]|⍵}
LeftChained←{⊃⍺⍺/(⌽⍺),⊂⍵}
Preprocess←{⍵+1E¯180×0=⍵}
Postprocess←{⍵×1E¯160<|⍵}
Postprocess(⍳⍴⍴⍵)AxialNormalize LeftChained⍣≡Preprocess ⍵
}
Normalize←{ ⍝ Normalize an array of arbitrary rank - Compatible version
AxialNormalize←{(⍵×⍺⊃⍴⍵)÷[(⍳⍴⍴⍵)~⍺]+/[⍺]|⍵}
LeftChained←{⊃⍺⍺/(⌽⍺),⊂⍵}
Until←{⍵ ⍵⍵ x←⍺⍺ ⍵:x ⋄ ∇ x}
Preprocess←{⍵+1E¯180×0=⍵}
Postprocess←{⍵×1E¯160<|⍵}
Postprocess{(⍳⍴⍴⍵)AxialNormalize LeftChained ⍵}Until≡Preprocess ⍵
}
(The Preprocess and Postprocess functions are required to circumvent zero division problems.)
This population chart illustrates the power of the method very clearly:
|
|
|
|
|
|
|
|
|
771223 | 766554 | 735755 | 719250 | 706449 |
|
|
788905 | 772940 | 772147 | 739547 | 722845 |
|
|
814425 | 789766 | 775918 | 773772 | 741235 |
|
|
799778 | 814674 | 792198 | 777811 | 775035 |
|
|
773303 | 799910 | 816966 | 794141 | 778756 |
|
|
782784 | 773740 | 802195 | 819000 | 794971 |
|
|
814607 | 782802 | 775663 | 803429 | 819102 |
|
|
833793 | 814593 | 784716 | 777074 | 803783 |
|
|
866345 | 834766 | 817082 | 786980 | 778263 |
|
|
954074 | 867444 | 837502 | 819359 | 788064 |
|
|
943186 | 955399 | 870230 | 840052 | 820427 |
|
|
970098 | 945001 | 958622 | 873253 | 841560 |
|
|
949410 | 972105 | 948491 | 961356 | 874970 |
|
|
933225 | 951793 | 975676 | 951535 | 963201 |
|
|
901858 | 935755 | 955683 | 979021 | 953449 |
|
|
900050 | 905014 | 940218 | 959420 | 981339 |
|
|
908955 | 904300 | 911412 | 945119 | 962594 |
|
|
936004 | 913630 | 910945 | 916538 | 948796 |
|
|
937447 | 942036 | 922226 | 917900 | 921679 |
|
|
950649 | 947452 | 955826 | 934459 | 927797 |
|
|
911786 | 963406 | 963199 | 969933 | 945735 |
|
|
908151 | 922857 | 978755 | 976442 | 980454 |
|
|
910085 | 920340 | 939322 | 992803 | 987005 |
|
|
905701 | 921590 | 936609 | 952985 | 1003813 |
|
|
890669 | 916064 | 936232 | 948860 | 962464 |
|
|
912320 | 898814 | 928552 | 946009 | 956147 |
|
|
931254 | 918245 | 909454 | 936263 | 951628 |
|
|
1029212 | 935974 | 927431 | 916169 | 940907 |
|
|
1144718 | 1032886 | 943227 | 933124 | 919707 |
|
|
1202052 | 1147340 | 1038983 | 947840 | 935548 |
|
|
1296324 | 1203587 | 1151707 | 1042534 | 949498 |
|
|
1362258 | 1296851 | 1207656 | 1154077 | 1043319 |
|
|
1398811 | 1362199 | 1299552 | 1209961 | 1154414 |
|
|
1439408 | 1398313 | 1364225 | 1300709 | 1209537 |
|
|
1450859 | 1438889 | 1399998 | 1364686 | 1300032 |
|
|
1477274 | 1450005 | 1440128 | 1400187 | 1363600 |
|
|
1469050 | 1476581 | 1450670 | 1439945 | 1398377 |
|
|
1424872 | 1468164 | 1476899 | 1450555 | 1438447 |
|
|
1404723 | 1424090 | 1468690 | 1476463 | 1448475 |
|
|
1368060 | 1403988 | 1424674 | 1468226 | 1474533 |
|
|
1326138 | 1367322 | 1404263 | 1424198 | 1466359 |
|
|
1261066 | 1325466 | 1367630 | 1403660 | 1422470 |
|
|
1238416 | 1260096 | 1325031 | 1366909 | 1401548 |
|
|
1210553 | 1237357 | 1259536 | 1324022 | 1364641 |
|
|
1177514 | 1208956 | 1236607 | 1258214 | 1321898 |
|
|
1161536 | 1176030 | 1207862 | 1234722 | 1256051 |
|
|
1128557 | 1159795 | 1174673 | 1205707 | 1232037 |
|
|
1133521 | 1126482 | 1157765 | 1172503 | 1202886 |
|
|
1113454 | 1131138 | 1124315 | 1155464 | 1169433 |
|
|
1123726 | 1110862 | 1128577 | 1121436 | 1152162 |
|
|
1087755 | 1120698 | 1108022 | 1125457 | 1117790 |
|
|
1003191 | 1084091 | 1117385 | 1104667 | 1121792 |
|
|
947557 | 999443 | 1080585 | 1113405 | 1100655 |
|
|
834565 | 943614 | 995557 | 1076523 | 1108775 |
|
|
742176 | 830302 | 939581 | 991293 | 1071635 |
|
|
987985 | 737949 | 826037 | 934937 | 986273 |
|
|
1006682 | 981853 | 733724 | 821345 | 929925 |
|
|
981990 | 999971 | 975354 | 729066 | 816200 |
|
|
1189781 | 975077 | 992976 | 968455 | 723816 |
|
|
1258458 | 1181002 | 968067 | 985523 | 960921 |
|
|
1235197 | 1247770 | 1171255 | 959970 | 976976 |
|
|
1153916 | 1223925 | 1236424 | 1161033 | 951271 |
|
|
1078082 | 1142454 | 1212233 | 1224590 | 1150029 |
|
|
1049741 | 1066784 | 1130839 | 1199711 | 1211778 |
|
|
1012960 | 1037232 | 1054855 | 1118264 | 1186400 |
|
|
940888 | 999448 | 1024140 | 1042034 | 1104720 |
|
|
757258 | 926714 | 985463 | 1010252 | 1028050 |
|
|
752064 | 744532 | 912376 | 970422 | 995364 |
|
|
762724 | 738522 | 731607 | 896637 | 954207 |
|
|
799984 | 747726 | 724474 | 717779 | 880013 |
|
|
770179 | 782641 | 732099 | 709693 | 703388 |
|
|
758324 | 752048 | 764629 | 715508 | 693668 |
|
|
695572 | 738595 | 732999 | 745642 | 697782 |
|
|
673646 | 676352 | 718511 | 712768 | 725229 |
|
|
655313 | 653544 | 656444 | 696700 | 691416 |
|
|
595573 | 633548 | 632558 | 634908 | 673450 |
|
|
568893 | 574342 | 610897 | 610122 | 613167 |
|
|
573642 | 545926 | 551956 | 587216 | 586192 |
|
|
574718 | 547767 | 521892 | 528378 | 561897 |
|
|
537637 | 545651 | 520874 | 496753 | 503089 |
|
|
384281 | 506703 | 515478 | 492383 | 469764 |
|
|
235001 | 360199 | 475438 | 483677 | 462122 |
|
|
210078 | 218196 | 335240 | 442751 | 450653 |
|
|
214385 | 193387 | 201446 | 309447 | 408189 |
|
|
255958 | 195477 | 177109 | 184069 | 282744 |
|
|
1635134 | 1612696 | 1540092 | 1451680 | 1374891 |
Differences between Products
The second sample will show you how to quantify the reasons for deviations in calculations. Though a standard solution already exists, by doing APL examinations we quickly find out that there is something wrong with it, and we can come to more meaningful and realistic results.
A pre-calculation in its simplest form consists of the addition of item expenses, each being a product of price × quantity. These can then be compared by a post-calculation against the actual prices and quantities.
The differences between pre- and post-calculation should desirably be expressible as components of the costs, as only those can get summarized.
|
Item |
Pre-Calculation |
Post-Calculation |
Diff. |
||||
|
Price |
Qty. |
Costs |
Price |
Qty. |
Costs |
||
| Bricks |
0.75 € |
165 pc |
123.75 € |
0.80 € |
135 pc |
108.00 € |
-15.75 € |
| Cement |
2.50 € |
5.0 lb |
12.50 € |
2.70 € |
6.0 lb |
16.20 € |
3.70 € |
| Sand |
0.30 € |
2.0 lb |
0.60 € |
0.40 € |
30.0 lb |
12.00 € |
11.40 € |
| Total |
|
136.85 € |
|
136.20 € |
-0.65 € |
||
Table 5: Bricklayer’s calculation
To determine the reasons for the differences, we need to do a more detailed analysis on a per item basis.
In the German literature about management-economics I found the chart below to explain the concept. (Sorry about not having found it in my English literature[1].)
The pre-calculated costs of an item are represented by the grey field. The difference to the post-calculated cost consists of three fields: one resulting from the difference in the price; one from the difference in quantity; and a third one is called mixed deviation.
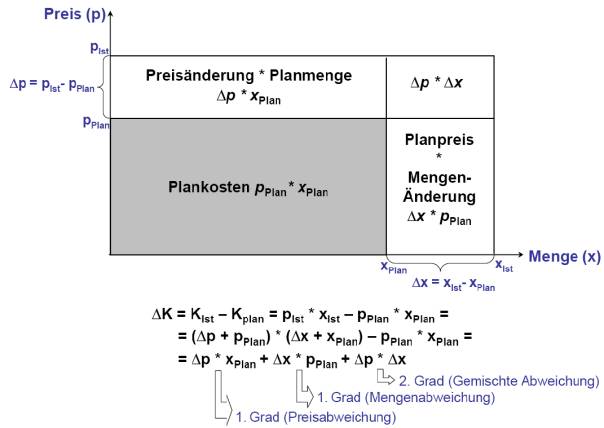
Chart 1: 1st grade and 2nd grade deviations
[Ref: Zitzmann, Betriebliches Rechnungswesen, Plankosten (chapter 9, page 31), Berner
Fachhochschule]
Differences in the prices are caused by inflation or other changes in the market. For differences in quantities the calculating person is responsible. Fortunately the third component, the mixed deviation, is not very much in this sample, so economists tend to neglect it.
Applied to the bricklayer sample, these differences may be separated into the three different causes:
|
Item |
Pre-Calculation |
Post-Calculation |
Differences by |
||||||
|
Price |
Qty. |
Costs |
Price |
Qty. |
Costs |
Price |
Qty. |
Mixed |
|
|
Bricks |
0.75 € |
165 pc |
123.75 € |
0.80 € |
135 pc |
108.00 € |
8.25 € |
-22.50 € |
-1.50 € |
|
Cement |
2.50 € |
5.0 lb |
12.50 € |
2.70 € |
6.0 lb |
16.20 € |
1.00 € |
2.50 € |
0.20 € |
|
Sand |
0.30 € |
2.0 lb |
0.60 € |
0.40 € |
30.0 lb |
12.00 € |
0.20 € |
8.40 € |
2.80 € |
|
Total |
|
136.85 € |
|
136.20 € |
9.45 € |
-11.60 € |
1.50 € |
||
Table 6: Bricklayer’s calculation with 1st grade and 2nd grade deviations
Though the total differences in the first table were as low as 65¢, they now expose as being 9.45€ and 11.60€, and furthermore having a mixed difference of 1.50€.
When exchanging the pre- and post-calculation values, peculiarly not only the deviations’ signs change, but also its values:
|
Item |
Post-Calculation |
Pre-Calculation |
Differences by |
||||||
|
Price |
Qty. |
Costs |
Price |
Qty. |
Costs |
Price |
Qty. |
Mixed |
|
|
Bricks |
0.80 € |
135 pc |
108.00 € |
0.75 € |
165 pc |
123.75 € |
-6.75 € |
24.00 € |
-1.50 € |
|
Cement |
2.70 € |
6.0 lb |
16.20 € |
2.50 € |
5.0 lb |
12.50 € |
-1.20 € |
-2.70 € |
0.20 € |
|
Sand |
0.40 € |
30.0 lb |
12.00 € |
0.30 € |
2.0 lb |
0.60 € |
-3.00 € |
-11.20 € |
2.80 € |
|
Total |
|
136.20 € |
|
136.85 € |
-10.95 € |
10.10 € |
1.50 € |
||
Table 7: Same as Table 6 with exchanged values for pre- and post-calculation
At this point, one began to have doubts about having found an appropriate solution for the problem. The situation worsens drastically when item costs are the result of three factors:
Costs = Price × Quantity × Rebate Factor [2]
In such cases you will get:
- One deviation based on price difference,
- One deviation based on quantity difference,
- One deviation based on rebate difference and
- Four mixed deviation components.
As it is not unusual that the sum of these four mixed components will be bigger than any of the three meaningful components, the usability of this method becomes rather questionable. So we must search for a better strategy.
To help you follow the quite terse functions, I will explain the resulting strategy for two factors first.
These are the conditions:
a × b + x + y = d × e
a × b + y = a × e
a × b + x = d × b
What we further need, are these two factors…
p = (b × d) E
q = (a × e) E
...to offer this solution:
x = (d - a) × (b + (e - b) × p / (p + q))
y = (e - b) × (a + (d - a) × q / (p + q))
With the exponent E=0, the mixed deviation is cut into halves:
x = (d - a) × (b + (e - b)/2)
y = (e - b) × (a + (d - a)/2)
With E=1, the bigger causer gets the bigger part of a deviation:
x = (d - a) × (b + (e - b) × (b × d) / ((b × d) + (a × e)))
y = (e - b) × (a + (d - a) × (a × e) / ((b × d) + (a × e)))
Here is the same as a dynamic function:
ProDiff←{E←1
b←⌽a←⍺+1E¯100
d←⍵+1E¯100
h←⌽g←d-a
q←⌽p←(d×b)*E
g×b+(h×p)÷p+q}
The additions in lines 2 and 3 are required to avoid division by zero.
These are the calculation results where the deviations are separated according to their origins.
|
Item |
Pre-Calculation |
Post-Calculation |
Differences by |
|||||
|
Price |
Qty. |
Costs |
Price |
Qty. |
Costs |
Price |
Qty. |
|
|
Bricks |
0.75 € |
165 pc |
123.75 € |
0.80 € |
135 pc |
108.00 € |
7.50 € |
-23.25 € |
|
Cement |
2.50 € |
5.0 lb |
12.50 € |
2.70 € |
6.0 lb |
16.20 € |
1.10 € |
2.60 € |
|
Sand |
0.30 € |
2.0 lb |
0.60 € |
0.40 € |
30.0 lb |
12.00 € |
1.60 € |
9.80 € |
|
Total |
|
136.85 € |
|
136.20 € |
10.20 € |
-10.85 € |
||
Table 8: Bricklayer’s calculation of two factors with E=0 (mixed component shared equally)
|
Item |
Pre-Calculation |
Post-Calculation |
Differences by |
|||||
|
Price |
Qty. |
Costs |
Price |
Qty. |
Costs |
Price |
Qty. |
|
|
Bricks |
0.75 € |
165 pc |
123.75 € |
0.80 € |
135 pc |
108.00 € |
7.40 € |
-23.15 € |
|
Cement |
2.50 € |
5.0 lb |
12.50 € |
2.70 € |
6.0 lb |
16.20 € |
1.09 € |
2.61 € |
|
Sand |
0.30 € |
2.0 lb |
0.60 € |
0.40 € |
30.0 lb |
12.00 € |
0.43 € |
10.97 € |
|
Total |
|
136.85 € |
|
136.20 € |
8.92 € |
-9.57 € |
||
Table 9: Bricklayer’s calculation of two factors with E=1 (appropriately shared to its causers)
With the exponent set to E=1 we get the best matching results, as it shares the mixed deviation component into parts appropriate to its cause.
As previously mentioned, these are calculation samples consisting of three factors. The four mixed deviations could get removed, and the calculation concept is symmetric. [3]
|
Item |
Pre-Calculation |
Post-Calculation |
Differences by |
||||||||
|
Price |
Qty. |
Reba. |
Costs |
Price |
Qty. |
Reba |
Costs |
Price |
Qty. |
Reba |
|
|
Bricks |
0.75 |
165 |
-12 % |
108.90 |
0.80 |
135 |
-16 % |
101.52 |
6.82 |
-21.17 |
6.97 |
|
Cement |
2.50 |
5.0 |
-5 % |
11.88 |
2.70 |
6.0 |
-16 % |
15.23 |
1.04 |
2.46 |
-0.14 |
|
Sand |
0.30 |
2.0 |
-20 % |
0.48 |
0.40 |
30.0 |
0 % |
12.00 |
1.49 |
8.87 |
1.17 |
|
Total |
|
|
|
121.26 |
|
|
|
128.75 |
9.34 |
-9.84 |
-7.99 |
Table 10: Bricklayer’s calculation of three factors with E=0 (mixed component shared equally)
|
Item |
Pre-Calculation |
Post-Calculation |
Differences by |
||||||||
|
Price |
Qty. |
Reba. |
Costs |
Price |
Qty. |
Reba |
Costs |
Price |
Qty. |
Reba |
|
|
Bricks |
0.75 |
165 |
-12 % |
108.90 |
0.80 |
135 |
-16 % |
101.52 |
6.73 |
-20.98 |
6.88 |
|
Cement |
2.50 |
5.0 |
-5 % |
11.88 |
2.70 |
6.0 |
-16 % |
15.23 |
1.03 |
2.46 |
-0.14 |
|
Sand |
0.30 |
2.0 |
-20 % |
0.48 |
0.40 |
30.0 |
0 % |
12.00 |
0.41 |
10.81 |
0.31 |
|
Total |
|
|
|
121.26 |
|
|
|
128.75 |
8.17 |
-7.72 |
7.04 |
Table 11: Bricklayer’s calculation of three factors with E=1 (appropriately shared to its causer)
In detail, 8.17€ of the difference are inflation based, -7.72€ are based upon the calculator’s fault, and 7.04€ are the result of a purchase manager who failed to ask for the discounts.
ProDiff←{ ⍝ Distribute differences to their causers
E←1
2=⍬⍴⌽⍴⍵:⍺{
b←⌽a←⍺+1E¯100
d←⍵+1E¯100
h←⌽g←d-a
q←⌽p←(d×b)*E
g×b+(h×p)÷p+q}⍵
3=⍬⍴⌽⍴⍵:⍺{
c←1⌽b←1⌽a←⍺+1E¯100
d←⍵+1E¯100
i←1⌽h←1⌽g←d-a
r←1⌽q←1⌽p←a*E
s←d*E
pt←1⌽rs←r×s
pu←2⌽qs←q×s
puq←1⌽rtp←1⌽qsr←qs×r
g×(b×c)+((h×c×qs)÷qs+pt) ...
+((i×b×rs)÷rs+pu) ...
+(h×i×qsr)÷qsr+rtp+puq}⍵
⍵-⍺
}
8 2⍕PreCalc
0.75 165.00 0.88
2.50 5.00 0.95
0.30 2.00 0.80
8 2⍕PostCalc
0.80 135.00 0.94
2.70 6.00 0.94
0.40 30.00 1.00
8 2⍕PreCalc ProDiff PostCalc
6.73 ¯20.98 6.88
1.03 2.46 ¯0.14
0.41 10.81 0.31
[1] Some translations: Preis = price; Menge = quantity; Preisänderung = price change; Planmenge = planned quantity; Planpreis = planned price; Plankosten = planned costs; Preisabweichung = deviation by price; Grad = grade; Mengenabweichung = deviation by quantity; Gemischte Abweichung = mixed deviation.
[2] Though a rebate is usually declared as a percentage, it is easy to transform into a multipliable component. e.g. 3.5% corresponds to a rebate factor of 0.965.
[3] This means, when exchanging the left and the right argument, the result will change its sign, not its values. When having three factors, the APL solution does not fulfil this requirement completely, because the full solution would be an iterative formula, which has been terminated at an acceptable precision.
October 2005
Peter-Michael HagerHAGER-ELECTRONICS GmbH
Hamburger Str. 97, 44135 Dortmund, Germany
email: hager@dortmund.net

